서울시 자전거 이용 예측모델을 만들 때 평가지표였던 RMSE에 대한 메모.
MAE (Mean Absolute Error)
실제 값과 예측 값의 차이를 절대값으로 변환 후 평균을 구한 것

* MAPE (Mean Absolute Percentage Error)
MAE를 비율로 나타냄으로써 스케일 의존적 에러를 보완.
하지만 실제값이 1보다 작거나 0일 때는 계산이 용이하지 않다는 단점이 있다.
* MASE (Mean Absolute Scaled Error)
예측 값과 실제 값의 차이를 평소에 움직이는 변동폭으로 나눈 값
평소 변동폭에 비해 얼마나 오차가 있는지를 나타냄
MSE (Mean Squared Error) 평균제곱오차
실제 값과 예측 값의 차이를 제곱해 평균한 것
제곱하기 때문에 이상치에 민감하다.

RMSE (Root Mean Squared Error) 평균제곱근오차
MSE에 루트를 씌운 값
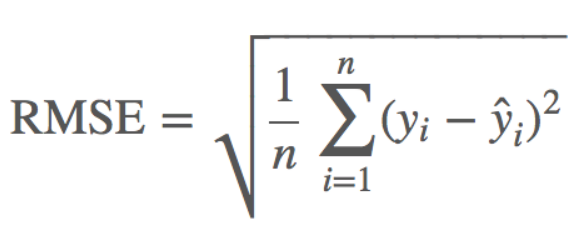
from sklearn.metrics import mean_squared_error
rmse = np.sqrt(mean_squared_error(y_test, y_preds))
# sklearn은 MSE만 지원하므로 이에 루트를 씌워서 RMSE 계산
* 스케일 의존 에러 (Scale-Depen-Error)
예를 들어, 실제 200만원인 삼성전자 주가를 예측할 때와 20만원인 네이버 주가를 예측할 때
RMSE가 동일하게 50이었다면 성능이 같다고 볼 수 있을까?
MAE, MSE, RMSE 는 이런 문제가 있음.
RMSLE (Root Mean Squared Log Error)
RMSE에 로그를 적용해준 지표.

* RMSLE는 Under Estimation에 큰 패널티를 부여한다.
예측값 = 600, 실제값 = 1,000일 때 >>> RMSE = 400, RMSLE = 0.510
예측값 = 1,400, 실제값 = 1,000일 때 >>> RMSE = 400, RMSLE = 0.33
값의 차이가 400으로 같고 RMSE가 동일하다.
하지만 RMSLE는 예측 값이 실제 값보다 작을 때 더 큰 값을 가진다.
* 배달 음식을 시킬 때, 30분이 걸린다고 고지하는 경우
실제 20분이 걸리는 건 큰 문제가 되지않지만 30분을 오버하는 건 문제가 될 수 있다. 이런 경우 적용 가능.
'노트1 > Python' 카테고리의 다른 글
| [Python] value_counts() 결과를 컬럼 순서대로 정렬하기 (0) | 2022.02.21 |
|---|---|
| [Python] selenium 크롤링 에러 : element not interactable (0) | 2022.01.21 |
| [Python] 서버에 HTTP 요청을 보내고(urllib/requests) Response에 접근하기(content/text) (0) | 2022.01.20 |
| [Python] matplotlib 정리 (0) | 2022.01.10 |
| [Python] 네이버 OPEN API 사용법 (네이버 블로그 크롤링, iframe, Selenium) (0) | 2021.12.14 |